Kapitel 1.1 - Atomarer Aufbau

Bohrsches Atommodell (Schalenmodell)

Jedes Atom besitzt einen Kern und eine Hülle. Im Kern befinden sich die positiv geladenen Protonen sowie die elektrisch neutralen Neutronen. In der Hülle bewege sich die negativen geladenen Elektronen. Jedes Proton und Elektron trägt eine Elementarladung.

Proton Neutron Elektron

Masse in 10^-24g 1,66 1,66 0,00091

Durchmesser in cm 10^-15 – 10^-14 10^-15 – 10^-14 10^-13 – 10^-12

Ladung in 10^-19 As +1,6 0 -1,6

Der Aufbau der Elektronenhülle ist für den chemischen Charakter eines Elements entscheidend, da sich alle Reaktion nur in der Hülle abspielen.
Die räumliche Verteilung der Elektronen um den Kern wird durch vier Quantenzahlen (Orbitalmodell) ausgedrückt.

Das Orbital oder Wolkenmodel

Es beschreibt die Aufenthaltswahrscheinlichkeit der Elektronen. Dabei können sich Elektronen nur in den rechtwinklig zueinander stehende Achsenrichtungen bewegen.

Hauptquantenzahl (n)

Die Hauptquantenzahl entspricht den Schalen im Bohrschen Atommodell 1, 2, 3, …. Maximal können sich n_s = 2 n² Elektronen auf der entsprechenden Schale aufhalten. Neben der numerischen Beschreibung der Hauptschalen kann diese auch mit Buchstaben erfolgen beginnend mit K, L, M, N, … Maximal aufgefüllte Schalen stellen einen energetisch stabilen Zustand dar.

Nebenquantenzahl (l)

Die Nebenquantenzahl oder auch Drehimpulsquantenzahl kennzeichnet die Form des Orbitals in einem Atom. Die Nebenquantenzahl kann werte von l=0 – (n-1) annehmen die auch mit römischen Kleinbuchstaben gekennzeichnet sind: s, p, d, f, g, … Die s Schale beschreibt eine Kugel, die p Schale eine einfache 8 die d Schale 2 kombinierte 8ten usw.

Magnetquantenzahl (m)

Die Magnetquantenzahl kann Werte von m= (-l) – l annehmen und beschreibt die räumliche Orientierung der Orbitale. Zum Beispiel die 3 Orbitale einer Unterschale p (l=1) sind in 3 Richtungen senkrecht zueinander in einem Rechtwinkligen Dreieck angeordnet p_x, p_y, p_z entsprechend den drei verschiedenen Werten von m=-1, 0, 1.

Spinquantenzahl (s)

Die Spinquantenzahl bestimmt die eigentliche Drehrichtung des Elektrons um sich selbst. S kann nur 2 Werte annehmen ±½.

Hundsche Regel

Beim Auffüllen der Elektronenschale werden zuerst die Elektronen mit parallelem Spin aufgefüllt, dann die mit Antiparallelem Spin. Bzw. es werden erst die Niveaus mit niedriger Energie Aufgefüllt.

Pauliprinzip

Innerhalb eines Atoms können niemals 2 Elektronen vorkommen, die in allen vier Quantenzahlen übereinstimmen.

Reihenfolge der Energieniveaus

Ab der 3. Periode überschneiden sich die Energieniveaus einer Unterschale mindestens mit den Energieniveaus der darüber liegenden Schale. Dies hat zur Folge, dass eine neue Schale besetzt wird, Während die darunterliegende noch nicht voll besetzt ist. Elemente mit dieser Elektronenkonfiguration nennt man Übergangselemente.

Kapitel 1.2 Bindungsarten

Atombindung – Kovalente Bindung – Elektronenpaarbindung

Hierbei handelt es sich um eine Verbindung von Nichtmetallen. Ihre Struktur wird durch bindende Elektronenpaare zusammengehalten. Ziel der Verbindung ist es Edelgaskonfiguration zu erreichen. Bei ungleichen Partnern könne sich die Ladungen verschieben. Auf diese Weise entstehen Dipole. Atome mit solch einer Bindung haben eine hohe Härte, hohe Schmelz- und Siedepunkte und eine Unlöslichkeit der Kristalle.

Ionenbindung

Die Ionenbindung entsteht durch die Anziehungskräfte von positiv und negativ geladenen Ionen. Hierbei handelt es sich um eine Verbindung von Metallen und Nichtmetallen. Das Metall gibt sein Elektron ab und wird zu einem Kation, das Nichtmetall nimmt das Elektron auf wird zu einem Anion. Durch diese unterschiedliche Ladung bleiben die Atome durch die Coulombkraft bei einander. Atome mit solch einer Bindung haben eine hohe Gitterenergie und damit hohe Schmelz- und Siedepunkte.

Metallische Bindung

Sie beschreibt die Bindung zwischen 2 Metallen. Dabei werden die Valenzelektronen abgegeben. Wenn viele Valenzelektronen abgegeben werden könne spricht man auch von einer Elektronen Delokation . Dabei befinden sich die Elektronen in einer Elektronenwolke.
Solche Verbindungen haben eine gute elektrische Leitfähigkeit, sind gute Wärmeleiter, besitzen einen metallischen Glanz und sind undurchsichtig.

Van der Waals Bindung

Sie ist die schwächste Bindung und wirkt zwischen Molekühlen. Es gibt zwei Arten. Zum einen die intermolekulare Dipol Bindung die als Ursache permanent elektrische Dipole vorweist und induzierte Dipol Wechselwirkungen, auch Dispersionsbindung, die auf Grund von momentanen Ladungssymmetrien entstehen. Diese Bindung wirk sich zumeist auf die physikalischen Eigenschaften aus.

Kapitel 1.3 Kristallstrukturen

Kristalline Verbände bilden atomare, ionische oder molekulare Verbände die sich gleichmäßig im Raum verteilen. Kristalline Stoffe haben eine feste Schmelztemperatur T_S bei der Sie flüssig werden. Mit steigender Temperatur nimmt das Volumen zu, welches sprungartig bei T_S ansteigt.
Amorphe Verbände sind Stoffe die keine geordnete Struktur aufweisen. Amorph heißt gestaltlos. Wie die kristallinen Verbände besitzen sie eine Schmelztemperatur und vergrößern mit steigender Temperatur ihr Volumen mehr als kristalline Verbände. Zusätzlich besitzen sei eine Glasübergangstemperatur T_G unterhalb von T_S wo sie beginnen zu fließen.
Bei beiden Verbänden singt mit steigender Temperatur das G-Modul wobei Amorphe Verbände einen zusätzlichen Sprung bei T_G aufweisen.

Elementarzellen und kubische Gitterstrukturen

Eine Elementarzelle ist die kleinste sich wiederholende Volumeneinheit im Gitteraufbau. Sie wird durch die Achsen und Winkel beschrieben.

Kubisch	a=b=c	α=β=γ=90°
Tetragonal	a=b≠c	α=β=γ=90°
Rhombisch	a≠b≠c	α=β=γ=90°
Hexagonal	a=b≠c	α=β=90°, γ=120°
Trigonal	a=b=c	α=β=γ≠90°
Monoklin	a≠b≠c	α=β=90°, γ≠90°
Triklin	a≠b≠c	α≠β≠γ≠90°

Gitterebene Millersche Indizes (hkl)

Sie dienen der eindeutigen Beschreibung von Richtungen und Ebenen. Besondere Bedeutung findet diese in der Kristallographi um Kristallflächen eindeutig zu beschreiben.
Vorgehensweise:
1. Lege einen Ursprung im Kristallgitter fest
2. Bestimme die Schnittpunkte mit den Koordinatenachsen
3. Bilde den Kehrwert
4. kleinsten Hauptnenner bilden. Die Zählerzahlen entsprechen den Millerschen Indizes

Jede so gebildete Ebene wird in runde Klammern geschrieben (hkl). Je nach Betrachtung können immer die selben Ebenen gemeint sein. Man kann diese dann zusammenfassend in geschweifte Klammern Schreiben {hkl}. Richtungen senkrecht auf einer Ebene stehen werden in eckige Klammern geschrieben [hkl] Welche wie bei den Ebenen zusammengefasst werden können zu spitzen Klammern <hkl>. Auf diese Weise lässt sich jede Richtung und Ebene eineindeutig beschreiben.

Dichteste Kugelpackung

Sie ist das Verhältnis von Volumen einer Elementarzelle zum Volumen der darin vorkommenden Atome.

Diamantstrukturen

Die Atome in einer Elementarzelle sind tetraedisch angeordnet. Wird eine solche Zelle planar angegeben. So schreibt man die Höhenlage eines Atoms als Bruch zwischen 0 und 1.

Gitterfehler

Nulldimensionale Gitterfehler - Punktfehler
Hierbei handelt sich um drei Arten von Fehler. Die Leerstellen, Zwischengitteratome und Fremdatomeinlagerung. Leerstellen und Zwischengitteratome hängt von der Temperatur ab und kann wie folgt berechnet werden:

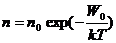
mit n₀ Anzahl der Atome pro Volumeneinheit, W₀ Energie zur Bildung eines Gitterfehlers und k die Bolzmannkonstante K=1,38 10^-23 J/K.
Eindimensionale Fehler - Linienfehler
Dies sind Linienförmige Fehler, Versetzungen, wie Stufen- oder Schraubenversetzungen. Ohne Versetzungen ist keine plastische Verformung möglich. Jede plastische Verformung erzeugt neue Versetzungen.
Zweidimensionale Fehler - Flächenfehler
Dies sind Grenzflächenfehler, Oberflächenfehler, Korngrenzen und Phasengrenzen
Korngrenzen sind Gitter mit gleicher Art von Atomen aber unterschiedlicher Raumorientierung die aufeinander treffen.
Phasengrenzen sind Gitter mit unterschiedlichen Atomarten und unterschiedlicher Raumorientierung, die aufeinander treffen, Wobei die Gitter völlig unlöslich im festen sind, sich also die verschiedenen Atome nicht mischen
Kleinwinkelkorngrenzen stehen in einem Winkel von unter 15° zueinander.
Dreidimensionale Fehler – raumförmige Fehler
Hierbei handelt es sich um Cluster, Ausscheidungen und Poren.
In Clustern kommt es in bestimmten Gittergebieten (Zonen) zur Anhäufung von Fremdatomen, ohne dass sich eine eigene Phase bildet.
Poren sind Ansammlungen von Leerstellen
Ausscheidungen sind eingelagerte oder oberflächliche Fremdatome.

Anisotropie und Texturen

Es gibt 3 Fälle von Isotropie (Unabhängigkeit der Eigenschaften von einer Richtung): Anisotropie ist das Gegenteil der Isotropie
Quasiisotrop ist Materie wenn sie Eigentlich nicht Isotrop ist jedoch makroskopisch Isotrop auftritt
Der wichtigste Parameter zur Beschreibung der Anisotropie polykristalliner Werkstoffe ist die Textur. Im Falle einer regellosen Textur, bei der alle Orientierungen. gleich häufig vorhanden sind, ist das Verhalten des polykristallinen Materials isotrop

Kapitel 1.4 Phasen und Zustandsdiagramme

Flüssig, fest, gasförmig – Keimbildung

Je nach Temperatur haben Werkstoffe einen anderen Aggregatszustand. Wird Energie in Form von Wärme zugeführt oder entnommen ändert sich dieser.
Hat ein Werkstoff viel Energie, also eine hohe Temperatur, liegt er in flüssiger Form vor, so entsteht beim abkühlen die Keimbildung. Je schneller der Werkstoff abgekühlt wird umso mehr Keime entstehen. An den Keimen werden Bindungen wiederaufgebaut und Atome verbinden sich. So bildet jeder Keim ein Gitter, dass gegenüber seinem Nachbarkeim eine andere Orientierung hat. So entstehen Korngrenzen.

Schmelzen und Erstarren

Der Energieerhaltungssatz besagt, dass die Wärmemenge für das Schmelzen eines Stoffes die gleiche ist wie beim erstarren mit unterschiedlichen Vorzeichen. Der Übergang von Fest in flüssige Form erfolgt langsam, so wie die Bindungsenergien zwischen den Atomen überwunden werden. Diese Temperatur heißt Schmelztemperatur T_S.

Binare Legierungen

Vollkommene Unlöslichkeit zweier Metalle im flüssigen und festen Zustand
Ist ein Stoff unlöslich, so bilden sich Gitterbereiche mit nur einer Art von Atomen. Die Stoffe sind koexistent. Somit haben beide Stoffe auch eine unterschiedliche Schmelztemperatur und während ein Stoff noch flüssig ist, kann der andere noch als Schmelze vorliegen.
Vollkommen löslich im festen und flüssigen Zustand
Lösliche Stoffe mischen sich in einer Schmelze und bilden beim Abkühlen eine gemeinsame Gitterstruktur. Es entsteht ein Mischkristall. Die Mischkristallbildung solcher Stoffe werden mittels Liquidius- Soliduslinen Linien in einem Diagramm dargestellt. Mittels Hebel-Gesetzt kann aus diesem Diagramm der Mengenanteil an Schmelze und Kristall berechnet werden.
Vollkommene flüssige Löslichkeit und vollkommene feste Unlöslichkeit
Diese Stoffe werden Eutektikum genannt. Der eutektische Punkt beschreibt das Mischungsverhältnis und die Temperatur bei der beide Stoffe gleichzeitig erstarren. Es entsteht ein α + β Mischkristall mit Lamellenstruktur. Mit Änderung der Konzentration von α + β werden zunehmend mehr Regionen mit α oder β Kristallen gebildet.

Kapitel 1.5 Leitungsmechanismen

Definition

Elektrische Leitfähigkeit im flüssigen. Hierbei handelt es sich um Ionenleitung. Ein im Wasser disoziierter Stoff z.B. NaCl, Hier wandern positiv geladene Atome zur Anode (Na⁺) und negativ geladene zur Kathode (Cl^-). Da sich hier ganze Atome bewegen spricht man auch von Stofftransport.
Elektrische Leitfähigkeit im festen. Dies ist ein Leitungsmechanismus ohne Stofftransport, da sich nicht die Atome sondern nur die Elektronen bewegen.

Leiter – Halbleiter – Isolatoren

Leiter weisen eine Leitfähigkeit von κ > 10³ S/cm auf. Halbleiter von 10³ < κ < 10^-4 S/cm und Isolatoren liegen bei κ < 10^-4 S/cm. Die Leitfähigkeit lässt sich berechnen:
Κ = e₀ n μ (n₀=Elementarladung 1,602*10^-19 C; n = Anzahl der frei beweglichen Elektronen; μ = Beweglichkeit der Elektronen) Bei Metallen ist n konstant und μ variabel. Die Konzentration von Leitungselektronen in Leitermetallen liegt bei 10²² /cm³.
Die Einteilung kann auch über den spezifischen Widerstand erfolgen. Es gilt U=I*R=I*ρ*l/A und somit κ = 1/ ρ

Beweglichkeit der Elektronen

Die mittlere Driftgeschwindigkeit v_d ist eine der allgemeinen Teilchenbewegung überlagerte, in eine bestimmte Richtung weisenden Geschwindigkeit.
Strom durch einen Leiterabschnitt I=Q/t = n*e₀*A*l/t; v_d=l/t=μ*E=μ*U/l=I/(n*e₀*A); μ = v_d/ E = v_d * l / U = κ / ( n * e₀).

Leitungsträgerkonzentration

Für Metalle, Halbmetalle und Halbleiter kann die Ladungsträgerkonzentration methematisch erfasst werden zu:
n = N_A* ρ / m_A = N_A/ V_m (N_A Avogadro 6*10²³; m_AAtomgewicht ρ = m_A / V_m = Dichte; V_mmolares Volumen = m_A / ρ)

Bändermodell

In einem einzelnen Atom existieren die Elektronen auf Energieniveaus mit definierten Energiebeträgen. In Festkörpern lagern die Atome so dicht aneinander, dass die Wechselwirkungen zwischen ihnen unbedingt berücksichtigt werden müssen, da es dadurch zu einer gegenseitigen Beeinflussung kommt.
Nähern sich z.B. 2 Atome so spaltet sich jedes Energieniveau zweifach auf (Bei 6 Atomen sechsfach). Die so entstandenen Energieniveaus liegen durch ihre geringe Energiedifferenz so dicht beisammen, dass sie praktisch ein Band bilden. Je weiter sich ein Niveau vom Atomkern weg befindet desto stärker ist die Spaltung. Dadurch entstehen Bänder die allen Atomen in Gitter gehören. Dieses Leitungsband Liegt oberhalb der Energie des Potentionalrichter W^*_R. Ist die Energie < W^*_R so sind die Elektronen am jeweiligen Kern lokalisiert. Zwischen den Bändern besteht kein gültiges Energieniveau. Dies ist eine verbotene Zone. Das oberste Band für das gilt E < W^*_R heißt Valenzband (VB), das Band für E > W^*_R heißt Leitungsband (LB). Eine Elektronenleitung ist nur in halb besetzten Bändern möglich. In vollbesetzten Bändern gibt es keinen Energiezustand der besetzbar ist.

Metalle und Isolatoren

Metallischer Leiter der ersten Art. Hier sind Grund- (VB) und Leitungsband (LB) beteiligt. Beide Bänder sind nicht voll besetzt. Al, Cu, Ag,…
Metallische Leiter der zweiten Art. Hier ist das letzte Band (VB) voll besetzt und lappt in das Leitungsband hinein. Somit verschwindet die Barriere zwischen VB und LB und Elektronen können fließen. Erdalkalimetalle.
Bei Isolatoren ist das VB voll besetzt und das LB ist leer. Die verbotene Zone ist breiter als 3eV. Somit können nur bei Zufuhr entsprechend hoher Energie oder durch hohe Temperaturen die Elektronen vom VB ins LB gelangen. (z.B. Durchschlag)
Halbleiter sind im Grunde Isolatoren wobei die verbotene Zone weniger als 3eV beträgt. Somit können Leitungselektronen schon bei geringer Anregungsenergie entstehen. Es liegt die Eigenhalbleitung oder intrinsiche Leitung vor. Die Generation ist der Übergang der Elektronen vom VB in das LB. Hierbei entstehen im LB Elektronen (n) und im VB Löscher (p). Beim fließen der Elektronen kommt es zu Wechselwirkungen mit dem Gitter und zu einem Energieverlust, so dass Elektronen wieder ins VB fallen. Dieser Prozess heißt Rekombination. Die Konzentration der Ladungsträger errechnet sich zu n_i² = n*p, wobei des thermodynamische Gleichgewicht besagt; n_i = n = p. Hieraus kann die Leitfähigkeit errechnet werden zu: κ= e₀*n* μ_n+e₀*p* μ_p=e₀*n_i*( μ_n+ μ_p).

Dotierung

Hierbei werden in das Halbleitergitter , Grundstoff hierfür ist Silizium, Fremdatome eingelagert um die Leitfähigkeit zu erhöhen.

n- Halbleiter

Es werden Elemente aus der 5. Hauptgruppe in das Si-Gitter eingelagert. Diese Gruppe heißt Donatoren. Mit 4 Elektronen wird eine Bindung mit dem Silizium eingegangen, das 5. Elektron bildet ein neues Energieniveau im verbotenen Bereich des Bändermodells. Mit einer geringen Energie E_d kann das Elektron in das Leitungsband angehoben werden. Bei der n-Dotierung gibt es mehr Majoritätsladungsträger (freie Elektronen) wie Minoritätsladungsträger (Löcher). Es gilt n = p + p_D (p_D Konzentration Donatoratomen) somit ist n >> p und es gilt κ ≈ e₀*n*μ.

p- Halbleiter

Hier werden Elemente der 3. Hauptgruppe, Akzeptoren, eingelagert. Dotierung mit 3-wertigen Atomen führt zu einer ungesättigten Bindung. Das fehlende Elektron kann mit geringem Energieaufwand E_a aus einer anderen Bindung gerissen werden. Es entsteht wiederum ein neues Band in der verbotenen Zone, jetzt jedoch oberhalb des VB. Jetzt sind die Elektronen die Minoritätsladungsträger und die Löscher die Majoritätsladungsträger. Somit gilt p >> n und κ ≈ e₀*p*μ.

Temperatureinfluss

Die Konzentration der frei beweglichen Elektronen ist temperaturabhängig und kann wie folgt berechnet werden: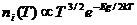

Wenn T ↑ →n(T) ↑ oder →μ ↓ oder → E_g ↑

n-p-Übergänge – Halbleiterdioden

Wenn zwei unterschiedlich dotierte Halbleitermaterialien zusammen gebracht werden, ohne das ein Feld am p-n-Übergang angelegt wird, so kommt es auf Grund er unterschiedlichen Ladungsträgerkonzentration in den beiden Schichten zu einer Diffusion der beweglichen Ladungsträger. (Konzentrationsausgleich). Aus der n-Zone wandern die Elektronen Richtung p-Zone und umgekehrt. Der so resultierende Diffusionsstrom ist vom Diffusionsgefälle abhängig (von der Stärke der Dotierung). Die Rekombination führt zu einem elektrischen Feld der Sperrschicht, dessen Ursache in den, im Gitter fest verankerten, Donatoren und Akzeptoren zu finden ist. Wird ein Feld in Sperrrichtung (Plus am n-Gebiet) angelegt, verstärkt sich diese Wirkung. Nur die noch nicht rekombinierten Minoritätsladungsträger könne sich noch bewegen, es fließt der geringe Sperrschichtstrom. Wird das Feld in Durchlassrichtung angelegt, so wird das Sperrschichtfeld gehemmt. Bei Si ist ab einer Spannung von 0,6 V diese Sperrschicht nicht mehr vorhanden.

Regel von Matthiesen

Elektrischer Widerstand setzt sich zusammen aus thermischen Anteil ρ_th und temperaturunabhängigen Anteil ρ_S: Der Anteil ρ_S wird durch die Streuung an der Gitterstruktur und Strukturdefekte erzeugt: ρ = ρ_th + ρ_S
ρ = C^αT α ist negativ wenn mit steigender Temperatur die Leitfähigkeit zu nimmt.

Reinheit, Legierungsarten

Allgemein gilt, je höher der Reinheitsgrad umso besser ist die Leitfähigkeit. Dies gilt auch bei Fremdatomeinlagerungen. Bilden die Komponenten einer Legierung eigene Phasen (Völlige Unlöslichkeit, dann hängt der spezifische Widerstand nahezu linear vom Volumenanteil der an der Legierung beteiligten Phasen ab. Besteht die Legierung aus völlig Löslichen Komponenten, ein Mischkristall, so sinkt die Beweglichkeit der Elektronen mit Zunahme der Streuung an Gitterfehlern. Wenn durch solch eine Legierung ein Strom fließt, so fliest ieser über den kompletten Querschnitt des Leiters (wünschenswert). Wohingegen bei teilweiser Löslichkeit (Lamellenstruktur bei Eutektikum) der Strom nur durch die Phasen mit dem geringern Widerstand fließt, Volumenanteilabhängigkeit.
Aus der Mattheisenschen Regel folgt das der Temperaturkoeffizient bei Mischkristallen kleiner ist. Und das Produkt aus Koeffizient und spezifischen Widerstand konstant ist.

Elektrische Leitfähigkeit an dünnen Schichten

Unterscheidet man einen Draht zu einer Schichtdicke d_S die dünner ist wie die mittlere Zitterbewegung der Elektronen (Leiterbahnen in Chips), so muss die Mattheisensche Regel um einen Widerstandsanteil erweitert werden: ρ = ρ_th + ρ_{S +} ρ_D. Bei allen Abscheidungen von Schichten auf einem Substrat gibt es Wechselwirkungen. Diese wirken innerhalb einer Grenzfläche zum Substrat und zur Umgebung. Abhängig vom Material muss ab der Unterschreitung einer Schichtdicke ρ_D beachtet werden: Au < 150 μm Cu < 300 μm.

Kapitel 1.6 Mechanische Verformung

Beanspruchungsarten

Dehnung (ε) – Zugspannung σ=F/A

Scherung – Schubspannung τ= Gγ

Verdichtung – Komression ΔV/V

Verdrillung – Torsion

Durchbiegung – Biegemoment

Reversible Verformung Formänderung verschwindet unmittelbar bzw. eine

bestimmte Zeit nach Beendigung der Krafteinwirkung. Der Körper kehrt in seine

ursprüngliche Gestalt zurück = Elastische Verformung

Irreversible Verformung: Formänderung bleibt nach Beendigung der

Krafteinwirkung erhalten = plastische Verformung

Elastische Verformung

Bei der elastischen Verformung ändern sich die Anstände und Achsenwinkel. Dabei erhöht sich der Energieinhalt des Gitters durch die aufgezwungene Spannung. Da jedes System bestrebt ist die niedrigste Energiestufe einzunehmen, kehren die Gitterbausteine nach der Entlastung wieder in ihren stabilen Zustand zurück. Bei der elastischen Verformung ändert sich der Widerstand des Werkstoffes auf Grund der Deformation des Gitters und damit wegen der Beweglichkeit der Leitungselektronen.

Materialkonstanten

Spannung ist Kraft pro Ausgangsfläche σ=F/A

Dehnung ist die Längenänderung pro Ursprungslänge ε=ΔL/L

Elastizitätsmodul ist Spannung pro Dehnung E= σ/ ε

Schubspannung ist Kraft pro Ausgangsfläche τ=F/A

Abscherung ist die Längenänderung pro Ursprungslänge γ=ΔL/L

Gleitmodul ist Schubspannung pro Abscherung G= τ/ γ

Poisson-Zahl

Die Possionzahl (Querkontraktionszahl) stellt die Längendehnung zur Querdehung ins Verhältnis ν= ε_d/ ε. Aus V=l*d*d = (l+Δl)(d-Δd)² Ausmultiplizieren, Produkte von Δ vernachlässigen folgt direkt ν < ½.

Alle 3 Größen hängen über E=2(1+ ν)G zusammen. Bei Metallen gilt E~ 10-350 GN/m² mit ν=0,3.

Spannung und Dehnung

Die Streckgrenze R_P trennt elastische von plastischer Verformung. Technisch entspricht dies einer Längenänderung eines Stabes um 0,2 %.

Die Maximale Zugfestigkeit ist die Festigkeitsgröße R_m. Sie beschreibt das Maximum in der Spannung Dehnungskurve ohne den veränderten Querschnitt zu beachten.

Die wahre Spannung k_f ist die Kraft pro wahre Fläche.

Plastische Verformung

Die Gleitebene in einem Metall bildet diejenige Ebene mit der dichtesten Atompackung und dem größten Schichtabstand. Die Gleitrichtung ist die Richtung mit dichtester Atompackung. In dieser Richtung benötigt das Gleiten der Atomschichten die geringste Energie. Das Kristallgitter hat somit einen Einfluss auf die Gleitebene und Gleitrichtung.

Verfestigung, Erholung, Rekristallisation

Mit steigendem Verformungsgrad nehmen die Zugfestigkeit und die Streckgrenze zu sowie die Leitfähigkeit und die Fläche ab. Nimmt man einen bestimmten Verformungsgrad und brennt diesen in einem Ofen so bildet sich über die Brenndauer nach der Erholung eine Rekristallisation und dann eine Kornvergrößerung aus. Damit nimmt die Streckgrenze wieder ab, die Leitfähigkeit und die Fläche zu.

Kaltverformung und Rekristallisation

Rekristallisation ist der Abbau von Gitterfehlern in Kristallen metallischer Werkstoffe durch Neubildung des Gefüges auf Grund der Keimbildung und des Kornwachstums. Die Festigkeit nimmt durch den Abbau von Versetzungen ab. Als Rekristallisationstemperatur T_Rmin wird diejenige Temperatur bezeichnet, bei der ein Werkstoff innerhalb einer Betrachtungszeit vollständig rekristallisiert. Es gilt T_Rmin ~ 0,4 T_S [K]

Kriechverhalten

Zone 1: Übergangskriechen – Verformung durch Dehnung – Versetzungen im Material

Zone 2: Stationäres Kriechen – Gleichgewicht zwischen Verformung und Rekristallisation

Zone 3: beschleunigtes Kriechen – Verformung >> als Rekristallisation – Werkstoff ermüdet und reißt irgendwann

Kapitel 1.7 – Polymerstrukturen

Kunststoffe, Polymere und Plaste

Der Baustein eines Kunststoffes ist ein Makromolekül, Es entsteht über Reaktionsmechanismen aus einzelnen Molekühlen, den Monomeren, mit unterschiedlichen Bauprinzipien.

Die im Makromolekühl gebunden Atome, überwiegend C und H, sind durch kovalente Bindungen fest miteinander verbunden. Zwischen den Molekühlen wirken Nebenvalente Bindungen , Van der Waal Bindungen. Sind die Molekühle durch Hauptvalenze miteinander verbunden, entsteht ein relativ starres Makromolekühl. Es gibt 3 Kunststoffarten die nach ihren Molekühlbindungen unterschieden werden:

Thermoplaste sind linear unverzweigte Kettenmolekühle die über Dipolbindung zusammenhalten. Sie erweichen beim Erwärmen.

Duroplaste sind räumlich vernetze Gefüge die über Atombindungen Zusammengehalten werden. Sie sind nicht schmelzbar, quellbar oder löslich und liegen bei Raumtemperatur zumeist als harte glasartige Stoffe vor.

Elastomere sind räumlich vernetzte weder schmelzbare noch lösliche aber quellbare Stoffe die bei Raumtemperatur ein gummielastisches Verhalten aufweisen.

Glasübergangstemperatur

Sind die Nebenvalenzen bei einer für den Kunststoff typischen Temperatur „eingefroren“, verhält sich dieser Spröde. Oberhalb der Glasübergangstemperatur T_G wird er formbar.

Festigkeit

In Abhängigkeit von der Anordnung der Makromolekühle ist ein typisches Verhalten der Festigkeit als Funktion der Temperatur zu beobachten. Durmomere bleiben dabei bis zu ihrer Zersetzung hart, Elastomere werden mit steigender Temperatur weicher, bis sie sich schließlich auch zersetzen. Thermoplaste reagieren extrem sensibel da sie bei Erwärmung flüssig werden.

Polymerbildung

Polymerisation nur bei Plastomeren (Termoplaste)

Einzelne Monomere mit Doppelbindungen werden mittels UV-Bestrahlung behandelt. Dabei brechen die Doppelbindungen auf und die Monomere reagieren miteinander. Somit entstehen lange Makromolekülketten.

Polykondesation bei Plastomere und Duromere

Die Polykondensation ist eine stufenweise Kondensationsreaktion, bei der viele Monomere unter Abspaltung einfach gebauter Moleküle (meist Wasser) Polymere gebildet werden. Damit ein Monomer eine Reaktion eingehen kann muss es mindestens zwei funktionelle Gruppen besitzen, die besonders reaktionsfreudig sind (-OH, -COOH, CO,…)Durch wiederholen von diesem Vorgang entstehen lange Makromolekühle.

Polyaddition bei Plastomeren und Duromeren

Die Polyaddition ist eine Form von Polymerbildung, die nach de Mechanismus der nucleophilen Addition von Monomeren zu Polyaddukten abläuft. Dabei werden verschiedenartige Moleküle mit mindestens zwei funktionellen Gruppen unter Übertragung von Protonen verknüpft. Bei dieser Art der Verknüpfung muss eine Sorte von Molekülen Doppelbindungen aufweisen. Im Verlauf ist die Polyaddition der Polykondensation sehr ähnlich, jedoch ohne das entstehen von niedermolekularen Nebenprodukten wie Wasser.

Polymerleiter

Da alle Bindungselektronen fixiert sind, sind Polymere zumeist Isolatoren. Treten regelmäßige Doppelbindungen auf, so kann ein gerichteter Elektronentransport erfolgen (z.B. Antistatische Verpackung)

Kapitel 1.8 – Magnetismus

Kenngrößen

Die magnetische Feldstärke H erzeugt das Magnetfeld. H = I*n / l

Die magnetische Flussdichte B gibt die stärke des Magnetfeldes an B₀=μ₀H

Permeabilität ist der Verstärkungsfaktor zum Vakuum μ= μ₀ μ_r mit μ₀=4pi10^-7

Magnetische Polarisation J ist die Flussdichte die von einem Stoff verursacht wird

J= μ₀* μ_r*H- μ₀*H

Die magnetische Suzeptibilität χ= μ_r-1

Magnetisierung M=J/ μ₀

Magnetismus

Bei Einwirkung eines äußeren magnetischen Feldes auf einen Werkstoff kommt es zur Wechselwirkung mit den Bahn- und Spinmomenten. Hat ein Atom in seinem Niveau zwei Elektronen, die laut Hundsche Regel unterschiedlichen Spin haben müssen, so heben sich die Spinmomente nach außen hin auf und es bleibt nur das Bahnmoment übrig. Entsprechend bei Werkstoffen mit nur einem Elektron in eiem Niveau entsteht nach außen hin zusätzlich ein Spinmoment.

Diamagnetismus

Ein äußeres Magnetfeld bewirkt ein Eindrehen des Bahnmomentes in Feldrichtung. Es werden Kreisströme induziert, die dem erzeugten Feld entgegen wirken. Ist dies die einzige Wechselwirkung (nur das Bahnmomente) so wird das Feld im Werkstoff geschwächt μ_r < 1 und χ<0

Paramagentismus

Besitzt ein Werkstoff unpaarige Elektronen, so kommt es zusätzlich zum Eindrehen der Bahnmomente noch zur Ausrichtung der Spinmomente in Feldrichtung. Das Feld wird vom Werkstoff verstärkt μ_r>1χ>0

Ferromagnetismus

Hierfür müssen vier Bedingungen erfüllt sein:

1. Innere Elektronenschale ist unvollständig besetzt

2. Unkompensierte Spins sind vorhanden

3. Atomabstand ist mindestens der dreifache Radius der nicht spinkompensierten Schale

4. Ohne äußere Einwirkung bildet sich spontane Magnetisierung – Weißsche Bezirke (Domänen). Sie sind durch Blochwände voneinander getrennt.

µ_r>>1 χ>>0

Magnetisierung

Solange kein äußeres Magnetfeld angelegt ist gibt es Weißsche Bezirke mit Blochwänden. Wird nun ein Feld angelegt. So beginnen sich alle Weißschen Bezirke in Feldrichtung auszurichten. Sind alle Domänen in Feldrichtung ausgerichtet, ist die Sättigung erreicht. Eine weitere Erhöhung des Feldes bleibt Ergebnislos.

Wird ein Werkstoff das erste Mal magnetisiert, so wird das Verhalten über die Neukurve erklärt. Bei kleinen Feldstärken können sich die Blochwände Verschieben wodurch sich die Domänen vergrößern. Ist eine Blochwand komplett aus den Weißchen Bezirken verschwunden, so ist der Werkstoff nach Wegnahme des äußeren Feldes irreversibel magnetisiert. Somit stellt die normale Magnetisierungskurve sich als Hysteresekurve dar.

Hartmagnetika

Dies sind Stoffe die nach abschalten eines äußeren Feldes ihr Magnetfeld aufrecht erhalten.. Sie weisen eine breite Hysterese auf, was bedeutet, dass viel Energie für eine Ummagnetisierung aufgebracht werden muss. Hartmagnetika gilt für Feldeinflüsse H > 30 kA/m. Durch Dotierung kann verhindert werden, dass sich Weißsche Bezirke ausrichten.

Weichmagnetika

Sie verhalten sich entsprechend entgegen den Hartmagnetika und verlieren ihre magnetische Wirkung. Für das äußere Feld sollte gelten H < 1kA/m.

Sättigung

Die magnetische Sättigung kann nach folgender Formel berechnet werden: J_S=µ₀M_S=µ₀µ_BN_Az mit µ_B Bohrsches Magneton = 9,27410*10^-24 J/T, N_A Avogadro-Konstante 6*10²³ Atome/mol und z=Anzahl der Magnetone.

Curie Temperatur

Abhängig von der Temperatur lassen sich Werkstoffe leichter magnetisieren. Die Schwelltemperatur die Curie Temperatur T_C, gibt an, ab welcher Temperatur ein ferromagnetischer Werkstoff paramagnetisch wird.

Χ= χ(T)=C/(T-T_C) mit C=Konstante

Kapitel 1.9 – Supraleitung

Elektrischer Widerstand bei tiefen Temperaturen

1. Supraleitung besteht darin, dass der elektrische Gleichstromwiderstand bei Unterschreitung einer Sprungtemperatur der Curie Temperatur T_C, diskontinuierlich auf Null fällt, Dies nennt man Supraleitung der ersten Art.
2. Im supraleitenden Zustand wird as Magnetfeld aus dem stromdurchflossenen Leiter verdrängt. Der supraleitenden Zustand kann durch eine äußeres Feld aufgehoben werden. Dies geschieht ab der kritischen Feldstärke H_C und der Effekt heißt Meissner-Ochsenfeld-Effekt. Harte Supraleiter, Supraleitung der zweiten Art, weist zwei kritische Feldstärken auf. Bei der unteren beginnt der Leiter vom Feld durchflossen zu werden. Es liegt jedoch noch Supraleitung vor. Bei der oberen kritischen Feldstärke bricht dann die Supraleitung ab.
3. Die kritische Stromdichte j_C begrenzt die Supraleitung ebenso wie die oben genannten Punkte.

Elektronenpaare (Cooper-Paare)

Bei Unterschreitung von T_C treten zwei Elektronen mit entgegengesetztem Spin und Impuls zu einem Elektronenpaar zusammen. Dieses Paar bewegt sich schließlich bei einwirken eines Impulses einheitlich in Feldrichtung. Während der Werkstoff supraleitend ist werden diese Elektronen nicht gestreut. Die Kohärenzlänge von Cooperpaaren (der Abstand ) beträgt 100nm bis 1000nm

Meissner-Ochsenfeld-Effekt – kritische Feldstärke

Während der Supraleitung verdrängt der Werkstoff das äußere magnetische Feld komplett. Über einem starken Magnetfeld wird der Werkstoff im supraleitenden Zustand schweben. Es gilt H_C/H₀=1-(T/T_C)².

Kapitel 1.10 – Dielektrische Polarisation

Kenngrößen

Plattenkondensator: E=U/d und Q=ε₀*A*E mit ε₀ = 8,85*10^-12

Verschiebungsdichte D = ε₀*E

In Materie D= ε₀*E+P = ε_R ε ₀*E

Polarisation P=( ε_r-1) ε₀*E=χ ε₀E

Elektrische Suszeptibilität: χ = ε_r-1

Kondensator

Die durch die Coloumbschen Kräfte im Dielektrikum erzeugte Ladungsverschiebung ist dem Potential U der erregenden Feldstärke E entgegenwirkt. Durch die in einem paraelektrischen Werkstoff orientierten Dipolmomente werden Ladungsträger kompensiert und es können weitere Ladungsträger aus der Spannungsquelle auf die Metallplatten fließen. Die Ladung Q des Kondensators wird damit größer: Q=C_SU. Bei konstanter Spannung steigt die Kapazität des Kondensators mit zunehmendem ε_r Somit gilt C_S = ε_r*C₀ . Da auch die Kapazität direkt proportional zur Fläche A der Kondensatorplatten und umgekehrt proportional zum Abstand ist folgt: C_S= ε₀ ε_r*A/d

Polarisation

Verschiebungspolarisation

Sie tritt als Elektronen und Ionenpolarisation auf. Elektronenpolarisation entsteht durch Verschiebung der negativen Elektronenhülle gegenüber dem positiven Kern. Dieser Effekt tritt bei jedem Werkstoff auf und ist reversibel. Bei einem Wechselfeld bis 10¹⁴ Hz können die Elektronen ohne Phasenverschiebung diesem folgen.

Ionenpolarisation

Sie tritt bei Isolatoren mit Ionengitter auf. Hierbei wird das Kationenuntergitter gegen das Anionenuntergitter verschoben. Dieser Effekt ist reversibel. Dabei können die Ionen einem Wechselfeld bis 10¹¹ Hz folgen. Dies liegt an der deutlich höheren Masse von Ionen im Gegensatz zu Elektronen

Orientierungspolarisation

Bei permanenter Anwesenheit von Dipolen im Dielektrikum kommt es zur Orientierungspolarisation in Feldrichtung. Sie kann bis zu einer Frequenz von ca. 10¹¹ Hz einem Wechselfeld folgen.

Frequenzabhängigkeit von ε_r

Die Permitivität ε _r =√n = ε_r.Dipol + ε_{r, Ion} + ε_r,Elektron ist frequenzabhängig. Ab Frequenzen oberhalb von 10¹¹ Hz hat ε_r,Dipol keinen Einfluss mehr und ab 10¹⁴ Hz wirkt nur noch ε_r,Elektron.

Dielektrischer Verlustfaktor

Wirkt auf einen Kondensator mit Dielektrikum eine Wechselspannung, dann ändert sich in diesem die Verschiebungs- oder Drehrichtung der Ladungsschwerpunkte. I takt der Frequenz ändern sich im Werkstoff die Polarisationsrichtungen und die Dipole beginnen zu schwingen. Diese Schwingung erzeugt Wärme, welche den Verlust darstellt. Die Änderung der Polarisationsrichtung erfordert Arbeit, die bei der Kondensatorspannung U durch den Wirkstrom I geleistet wird. Somit gilt tan δ = I_V/I_C oder bei einer Parallelschaltung von Kondensator und Widerstand tan δ = I_R/I_C und es gilt: N_V=U²*2π*f* ε₀* ε_R*tan δ. Somit kommt bei einem leitenden Dielektrikum ein imaginärer Summand hinzu ε_r = ε₁ + jε₂ und es gilt weiter tan δ = ε₂/ε₁.

Einteilung der Dielektrika

Alle ferroelektrischen und nicht ferroelektrischen Werkstoffe sind pyroelektrisch. Alle pyro- und nicht pyroelektrische sind piesoelektrisch und diese komplemente zählen zu den dielektrischen.

Ferroelektrische Hysterese

Ein besonderer Fall bei der Orientierungspolarisation ist die spontane Polarisation die das ferroelektrische Verhalten Verursacht. Entgegen der Wärmeschwingung der Dipole, die ihre völlig gleichsinnige Orientierung verhindern, kommt es in Ferroelektrika, unter bestimmten strukturellen Bedingung zu Gleichgesinnung der Dipole. Diese Gebiete nennt man Domänen. Sie entsprechen den Weißschen Bezirken in ferromagnetischen Werkstoffen. Durch anlegen eines äußeren Feldes kommt es zur gleichsinnigen Orientierung der Domänen bis hin zur Sättigung.

Piezoelektrischer Effekt

Wird ein Piezoelektrisches Material mechanisch belastet, so führt dies zu einer Verformung der Gitterstruktur und zu einer Polarisation. Sogleich werden dann die Außenflächen geladen. Dieser Effekt heißt Piezoelektrisch.

F*Δx=Q*U = δ*A* Δx mit D=Q/A und d= Δx/U folgt D= δ*d.

Nichtferroelektrische Phasenübergänge

Bei hohen Temperaturen wird das Material paraelektrisch. Bei Abkühlung findet ab einer Schwelltemperatur kleiner der der Aufheizung ein Phasenübergang mit Struktur Veränderung statt und das material wird wieder ferrorelektrisch. Die Polarisationsrichtung kann durch eine äußeres Feld verändert werden.

2.x – Hall Effekt – Hall Generator

Der Hall-Effekt tritt in einem stromdurchflossenen elektrischen Leiter auf, der sich in einem Magnetfeld befindet, wobei sich ein elektrisches Feld aufbaut, das zur Stromrichtung und zum Magnetfeld senkrecht steht und das die auf die Elektronen wirkende Lorentzkraft kompensiert.